CMU 15-445 Database Systems

Lecture #08: Tree Indexes

Table Indexes

• 数据库中常常需要数据库的部分有序(这也是为什么哈希表做不成索引，因为无序)副本来提高查找的效率，这个副本一般称为索引
• DBMS要自己维护索引和数据的一致性，还有执行SQL的时候使用什么索引

B+ Tree

• B+ Tree是一种自平衡搜索树，它可以将查找的复杂度控制在$O(logn)$，同时它的设计也减小了查找时磁盘的$I/O$，这对于DBMS的效率来说是十分重要的
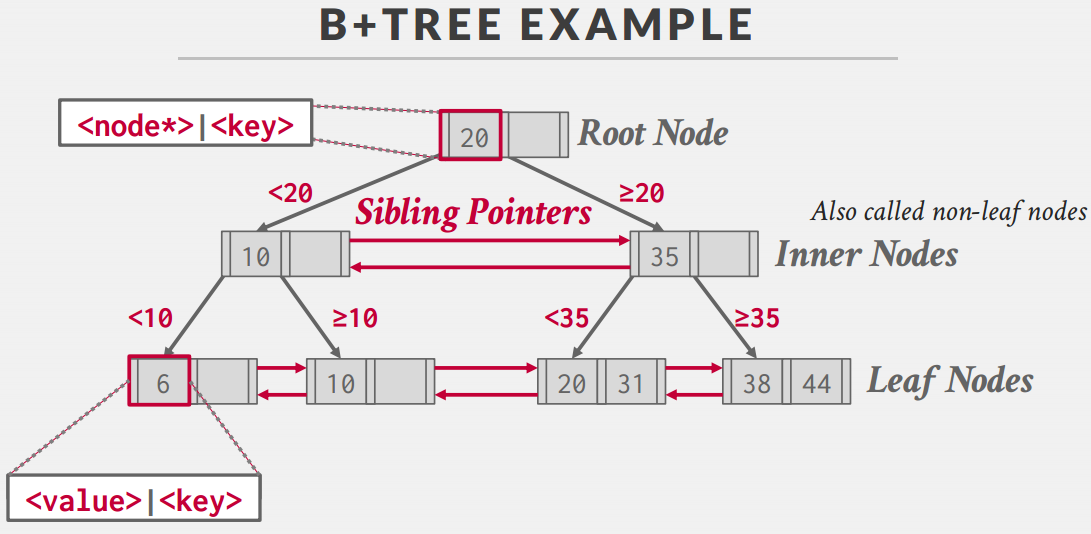
• 几乎所有支持索引的现代DBMS都用了B+ Tree，B+ Tree和B Tree最大的区别在于B+ Tree之有叶子节点才存储了值，非叶子节点存储的是部分索引的值，而B Tree的每个节点都存储了值

• B+ Tree有以下特点

  • 它是完全平衡的（所有的叶子节点高度一致）
  • 除了根节点外，每个内部节点至少为半满($\frac{M}{2}-1 \le num\ of\ keys \le M -1$)
  • 每个有K个键的节点有K+1个非空子节点（指针是从两个key中间的“缝”出来的）

• B+ Tree的每个节点都包含一个Key-Value的数组<索引值，下层的节点>

• B+ Tree的叶子节点有两种存储模式

  • 一种是存储Tuple的指针，通过这个指针去拿Tuple的数据
  • 另一种是存储Tuple的数据，这样就可以直接获取，不用再去找一次Tuple的数据

• 根据NULL在不同类型中的意义，NULL节点一般会在第一个或最后一个叶子节点里面（要看对NULL认为是无穷大的还是无穷小的）

• Insertion
  • 向下遍历树，找到插入的位置
  • 如果索引有足够的空间，则直接插入
  • 否则最下面的索引分裂，然后重新整合B+ Tree的结构后再插入

• Deletion
  • 如果删除后的节点少于半满，需要合并树

• Composite Index
  • 多个属性组成的联合索引

1

CREATE INDEX abc_index ON table (a, b, c);

• 我们可以使用联合索引来加快查询速度

1
2

SELECT a, b, c FROM table
WHERE a = 1 AND b = 2 AND c = 3;

• Selection Conditions

  • 要看联合索引的结构，是前面的字段先有序之后再排下一个字段，要想高效利用联合索引就要会最左匹配

• Duplicate Keys:重复索引的处理方法
  • append record IDs:后面加上唯一标识符。比如主键或者(page,slot)的元组，这样就保证绝对唯一
  • overflow nodes:给叶子节点再挂一个溢出节点，专门放碰撞的Key，但是增加了维护树结构的成本

• Clustered Indexes
  • 主键B+ Tree的叶子节点对应的数据就是实际数据，这样遍历到主键的话直接就拿到数据
  • 但是如果不是主键的B+ Tree的话，只能先拿到主键再去主键的B+ Tree上面找

• Index Scan Page Sorting
  • 先扫描统计要那些主键对应的数据，再把数据做一次排序 ,然后进主键的B+ Tree一把搜出来

B+Tree Design Choices

• Node size
  • 磁盘越慢，B+ Tree的节点越大，这样减少I/O的压力，如果是内存，节点应该变小，因为这个时候筛选无用数据的成本已经高过磁盘中的I/O了
    • HDD: ~1MB
    • SSD: ~10KB
    • In-Memory: ~512B
  • 还有就是业务类型，OTAP喜欢点查询，节点小一点好，OLAP喜欢动不动扫描全表，节点大一点好

• Merge Threshold
  • 一般来说合并拆分这种操作DBMS都是尽量拖一拖，因为这个过程开销太大了，所以不是到了阈值就马上合并

• Variable Length Keys
  • pointers:节点存指针
  • Variable Length Nodes:节点本身就是变长的，维护更加困难
  • Padding:数据不到规定大小，填充字节补偿(像字节对齐)
  • Key Map/Indirection:和slot很像，里面的结构加上slot-array来适应不同长度的数据

• Intra-Node Search
  • 节点内部的数据怎么搜索
    • Linear:线性遍历，看似低效，但是和I/O的时间比起来不算什么
    • Binary:二分，复杂度降为$O(log(n))$
    • Interpolation:利用数学规律/机器学习等其他方式进行推断查找

Optimizations

• Prefix Compression

  • 找前缀一样的统一存一下前缀，剩下的空间存后缀

  • 

• Deduplication
  • 一个K，后面根据所有的V，防止K冗余
  • $(K_1,V_1),(K_1,V_2),(K_1,V_3),(K_2,V_4),(K_2,V_5) \rightarrow\ (K_1,V_1,V_2,V_3),(K_2,V_4,V_5)$

• Suffix Truncation
  • 如果搜索的时候不要要全部数据往下走，只需要部分数据，那我存个前缀也行
    • 比如string的like”x%”这种操作，存前缀就够了

• Bulk Insert
  • 一次插入一批，减少树的分裂合并次数