Go 1.19 排序算法
Go 1.19 排序算法-$pdqsort$
三种经典排序算法的对比
- 所有短元素和元素有序的情况下,插入排序性能最好
- 在大部分情况下,快速排序都有较好的综合性能
- 几乎在任何情况下,堆排序都表现的比较稳定
- 能否结合上面三种排序算法的优点,设计出一个排序算法使得
$$ \begin{align} &Best \Longrightarrow O(n)\newline &Avg \Longrightarrow O(n\log n)\newline &Worst \Longrightarrow O(n\log n)\newline \end{align} $$
pdqsort
- 简介
$pdqsort(pattern-defeating-quicksort)$
是一种不稳定的混合排序算法,它的不同版本被应用在
C++ Boost,Rust以及Go1.19中。它对常见的序列类型做了特殊的优化,使得在不同条件下都拥有不错的性能
- 复习不稳定:$96_a,96_b \rightarrow^{sort} 96_b,96_a$
version 1
-
结合三种排序的优点
- 短序列使用插入排序
- 其他情况使用快排
- 如果快速排序表现不佳,则使用堆排序保证$Worst$情况下仍有$O(n\log n)$的复杂度
-
Q&A
- 短序列的具体长度是多少?
- 12~32,不同语言和场景下会有不同,在泛型版本中根据测试选定为24
- 怎么得知快排表现不佳,切换到堆排序?
- 当最终的$pivot$的位置离序列两端很接近时$(< \frac{length}{8})$(其实就是分的太少),判定其表现不佳,当这种情况达到$limit(bits.Len(length))$时,切换到堆排序
- 短序列的具体长度是多少?

- 改进:
choose pivot尽量能够选中中位数,改进choose pivot
version 2
-
version1中选择pivot的方式是选择首个元素,算法简单但是效率低 -
遍历数组,寻找真正的中位数 $\Longrightarrow$ 遍历代价太高
-
平衡
- 寻找
pivot所需要的开销 pivot带来的性能优化
- 寻找
-
解决方案
- 寻找近似中位数
-
根据不同的长度选择
pivot策略- 短序列$(\le 8)$:选择固定元素
- 中序列$(\le 50)$:采样选用三个元素,
median of three - 长度列$(>50)$:采样九个元素,
median of medians
-
pivot的采样方式可以让我们“感知”当前序列的状态- 采样都为逆序 $\Longrightarrow$ 猜测当前序列可能为逆序 $\Longrightarrow$
reverse(array) - 采样都为顺序 $\Longrightarrow$ 猜测当前序列可能为顺序 $\Longrightarrow$
insertsort(array)- 注:这里面的插入排序实际使用的是
partiallnsertionSort,即有限制次数的插入排序,来限制其最坏情况
- 注:这里面的插入排序实际使用的是
- 采样都为逆序 $\Longrightarrow$ 猜测当前序列可能为逆序 $\Longrightarrow$
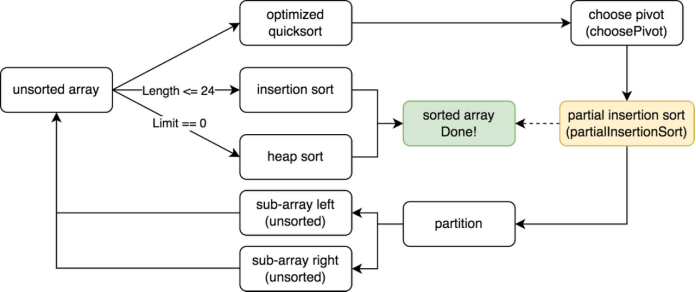
- 改进
- 优化了
pivot的选择策略(近似中位数) - 根据采样来感知序列状态,适当使用其他方法来提高收益(
reverse和partiallnsertionSort)
- 优化了
final version
-
还有什么情况没有被考虑到,可以被优化?
- 重复度较高
-
可以在选择
pivot的时候“感知”重复度?- 不是很好,因为采样不是很多,很难拿到相同的元素
-
解决方案
- 如果两次
partion生成的pivot相同,即对partition进行了无效分割,此时认为piovt的值为重复元素(比上面的方法有更高的采样率)
- 如果两次
-
优化-重复元素较多的情况(
partitionEqual)- 当检测到此时的
pivot和上次相同时 (发生在leftSubArray) ,使用partitionEqual将重复元素排列在一起,减少重复元素对于pivot选择的干扰
- 当检测到此时的
-
优化-当
pivot选择策略表现不佳时,随机交换元素- 避免一些极端情况使得
QuickSort总是表现不佳,以及一些黑客攻击情况(随机交换来增加不确定性)
- 避免一些极端情况使得
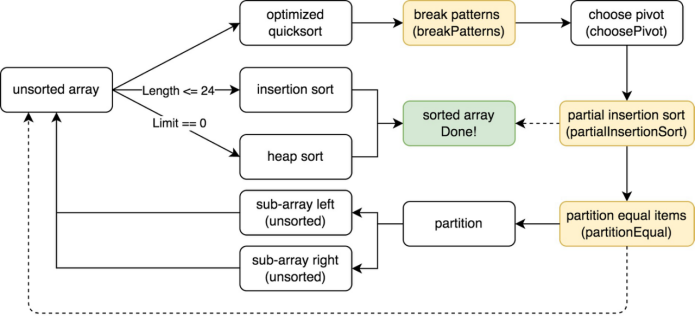
- 最终效果
$$ \begin{align} &Best \Longrightarrow O(n)\newline &Avg \Longrightarrow O(n\log n)\newline &Worst \Longrightarrow O(n\log n)\newline \end{align} $$
总结
-
高性能的排序算法是如何设计的?
- 根据不同情况选择不同策略,取长补短
-
生产环境中使用的的排序算法和课本上的排序算法有什么区别?
- 理论算法注重理论性能,例如时间、空间复杂度等。生产环境中的算法需要面对不同的实践场景,更加注重实践性能
-
Go 语言($\le 1.18$)的排序算法是快速排序么?
- 实际一直是混合排序算法,主体是快速排序。$Go \le 1.18 $时的算法也是基于快速排序,和
pdgsort的区别在于fallback时机、pivot选择策略、是否有针对不同pattern优化等
- 实际一直是混合排序算法,主体是快速排序。$Go \le 1.18 $时的算法也是基于快速排序,和
-
附
Go 1.20$pdqsort$源码
|
|
-
github上面的提交:https://github.com/golang/go/issues/50154
Go的源码还是不错的,起码不至于像C++那样群魔乱舞,考完试抽时间看看