CMU 15-445 Lecture #01: Course Overview & Relational Model
CMU 15-445 Database Systems
Lecture #01: Course Overview & Relational Model
Outline
- Course Logistics
- Relational Model
- Relational Algebra
Course overiew
- This course is about the design/implementation of database management systems (
DBMSs) - This is not a course ($\rightarrow Key\ point\ is\ the\ theory\ and\ the\ concept$) about how to use a DBMS to build applications or how to administer a DBMS.→ See CMU 95-703 (Heinz College)
PROJECTS
-
All projects will use the CMU DB Group BusTub academic DBMS.
- → Each project builds on the previous one.
- → We will not teach you how to write/debug C++17
-
complete Project #0 ! ! !
Database
-
Organized collection of inter-related data that models some aspect of the real-world
-
Databases are the core component of most computer applications
Example
Create a database that models a digital music store to keep track of artists and albums
- Things we need for our store
- Information about
Artists - What
Albumsthose Artists released
- Information about
FLAT FILE STRAWMAN
-
Store our database as comma-separated value (CSV) files that we manage ourselves in our application code
-
Use a separate file per entity
-
The application must parse the files each time they want to read/update records
-
-
Create a database that models a digital music store
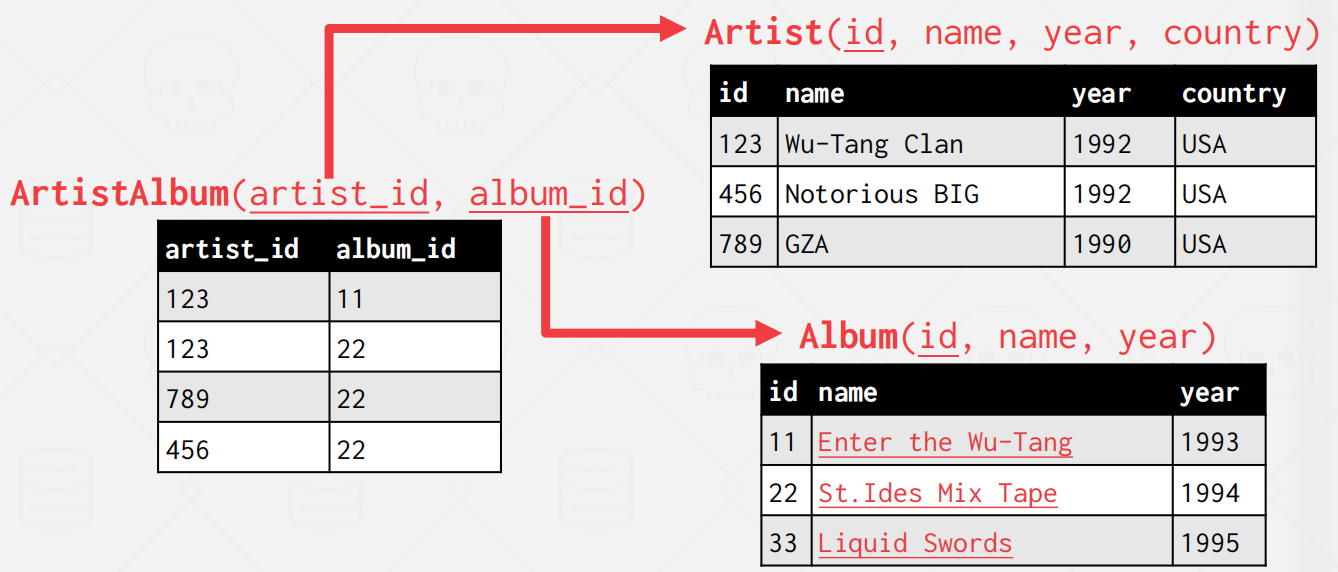
Artist(name, year, country)
|
|
Album(name, artist, year)
|
|
Our Code
- Example: Get the year that GZA went solo $\rightarrow$ Artist
|
|
Problem about FLAT FILES $\rightarrow$ DATA-INTEGRITY
-
How do we ensure that the artist is the same for each album entry?
-
What if somebody overwrites the album year with an invalid string?
-
What if there are multiple artists on an album?
-
What happens if we delete an artist that has albums?
Problem about FLAT FILES $\rightarrow$ IMPLEMENTATION
-
How do you find a particular record?
-
What if we now want to create a new application that uses the same database?
-
What if two threads try to write to the same file at the same time?
Problem about FLAT FILES $\rightarrow$ DURABILITY
-
What if the machine crashes while our program is updating a record?
-
What if we want to replicate the database on multiple machines for high availability?
DATABASE MANAGEMENT SYSTEM
-
A database management system (DBMS) is software that allows applications to store and analyze information in a database
-
A general-purpose DBMS supports the definition, creation, querying, update, and administration of databases in accordance with some data model
EARLY DBMSs
Early database applications were difficult to build and maintain on available DBMSs in the 1960s
Examples: IDS, IMS, CODASYL
Computers were expensive, humans were cheap😂
- Tight coupling between logical and physical layers
- Programmers had to (roughly) know what queries the application would execute before they could deploy the database😟
Ted Codd was a mathematician working at IBM Research in the late 1960s
He saw IBM’s developers spending their time rewriting database programs every time the database’s schema or layout changed😨
Devised the relational model in 1969
RELATIONAL MODEL
-
The relational model defines a database abstraction based on relations to avoid maintenance overhead
-
Key tenets
- Store database in simple data structures (relations)
- Physical storage left up to the DBMS implementation
- Access data through high-level language, DBMS figures out best execution strategy
-
Structure: The definition of the database’s relations and their contents
-
Integrity: Ensure the database’s contents satisfy constraints
-
Manipulation: Programming interface for accessing and modifying a database’s contents
- A relation is an unordered set that contain the relationship of attributes that represent entities
- A tuple is a set of attribute values (also known as its domain) in the relation
- Values are (normally) atomic/scalar
- The special value NULL is a member of every domain (if allowed)
Artist(name, year, country)
| name | year | country |
|---|---|---|
| Wu-Tang Clan | 1992 | USA |
| Notorious BIG | 1992 | USA |
| GZA | 1990 | USA |
$$ n-ary\ Relation=Table\ with\ n\ columns\newline $$
RELATIONAL MODEL: PRIMARY KEYS
- A relation’s primary key uniquely identifies a single tuple
- Some
DBMSsautomatically create an internal primary key if a table does not define one - Auto-generation of unique integer primary keys
- → SEQUENCE (SQL:2003)
- → AUTO_INCREMENT (MySQL)
| id | name | year | country |
|---|---|---|---|
| 123 | Wu-Tang Clan | 1992 | USA |
| 456 | Notorious BIG | 1992 | USA |
| 789 | GZA | 1990 | USA |
RELATIONAL MODEL: FOREIGN KEYS
- A foreign key specifies that an attribute from one relation has to map to a tuple in another relation
DATA MODELS
-
A data model is a collection of concepts for describing the data in a database
-
A schema is a description of a particular collection of data, using a given data model
-
Example
-
Relational $\leftarrow This\ Course\newline$
-
Key/Value
-
Graph
-
Document / Object
-
Wide-Column / Column-family
-
Array / Matrix / Vectors
-
Hierarchical
-
Network
-
Multi-Value
-
DATA MANIPULATION LANGUAGES (DML)
-
Methods to store and retrieve information from a database
-
Procedural:
- → The query specifies the (high-level) strategy to find the desired result based on sets / bags $\leftarrow Relational\ Algebra\newline$
-
Non-Procedural (Declarative):
- → The query specifies only what data is wanted and not how to find it. $\leftarrow Relational\ Calculus\newline$
RELATIONAL ALGEBRA
-
Fundamental operations to retrieve and manipulate tuples in a relation
- → Based on set algebra
-
Each operator takes one or more relations as its inputs and outputs a new relation
- → We can “chain” operators together to create more complex operations
$$ \begin{align} &\sigma\Longrightarrow Select\newline &\prod\Longrightarrow Projection\newline &\cup\Longrightarrow Union\newline &\cap\Longrightarrow Intersection\newline &-\Longrightarrow Difference\newline &\times\Longrightarrow Product\newline &\bowtie\Longrightarrow Join\newline \end{align} $$
SELECT
-
Choose a subset of the tuples from a relation that satisfies a selection predicate
-
Predicate acts as a filter to retain only tuples that fulfill its qualifying requirement
-
Can combine multiple predicates using conjunctions / disjunctions
-
$$ Syntax:\sigma_{predicate}(R) $$

|
|
PROJECTION
-
Generate a relation with tuples that contains only the specified attributes
-
Can rearrange attributes’ ordering
-
Can manipulate the values
-
$$ Syntax:\prod_{A_1, A_2, …A_n}(R) $$

|
|
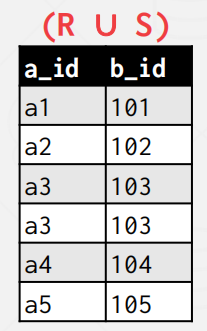
UNION
- Generate a relation that contains all tuples that appear in either only one or both input relations
$$ Syntax:(R\cup S) $$

|
|
INTERSECTION
- Generate a relation that contains only the tuples that appear in both of the input relations
$$ Syntax:(R\cap S) $$

|
|
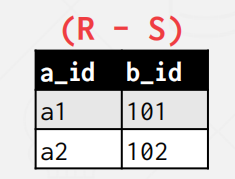
DIFFERENCE
- Generate a relation that contains only the tuples that appear in the first and not the second of the input relations
$$ Syntax:(R-S) $$

|
|
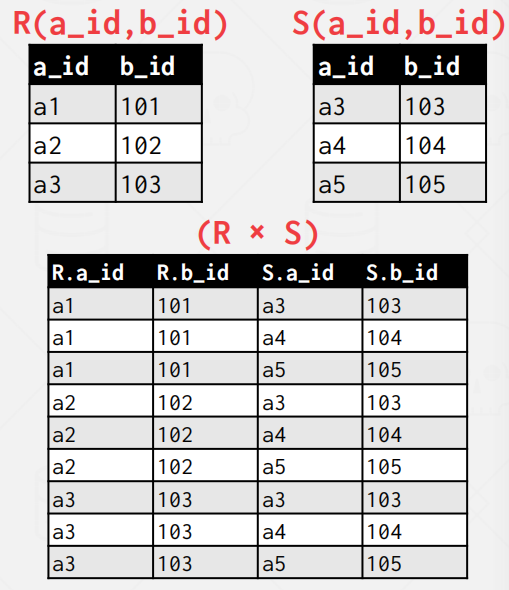
PRODUCT
- Generate a relation that contains all possible combinations of tuples from the input relations(
combination)
$$ Syntax:(R\times S) $$
|
|
JOIN !
- Generate a relation that contains all tuples that are a combination of two tuples (one from each input relation) with a common value(s) for one or more attributes
$$ Syntax:(R\bowtie S) $$
|
|
- R
| A | B |
|---|---|
| a | 1 |
| b | 2 |
- S
| B | C |
|---|---|
| 1 | x |
| 1 | y |
| 3 | z |
- $R\bowtie S$
| A | B | C |
|---|---|---|
| a | 1 | x |
| a | 1 | y |
|
|

EXTRA OPERATORS
-
Rename($\rho$)
-
Assignment($R \leftarrow S$)
-
Duplicate Elimination($\delta$)
-
Aggregation($\gamma$)
-
Sorting($\tau$)
-
Division($R\div S$)
OBSERVATION
Relational algebra is a procedural language because it defines the high level-steps of how to compute a query. For example, $\sigma_{b_id=102}(R\bowtie S)$ is saying to first do the join of R and S and then do the select,whereas $(R \bowtie (\sigma_{b_id=102}(S)))$ will do the select on S first, and then do the join. These two statements will actually produce the same answer, but if there is only 1 tuple in S with b_id=102 out of a billion tuples, then$(R \bowtie (\sigma_{b_id=102}(S)))$ will be significantly faster than $\sigma_{b_id=102}(R\bowtie S)$😂
A better approach is to say the result you want (state $\rightarrow$retrieve the joined tuples from R and S where b_id equals 102), and let the DBMS decide the steps it wants to take to compute the query. SQL will do exactly this,and it is the de facto standard for writing queries on relational model databases🐮
QUERIES
-
The relational model is independent of any query language implementation.
-
SQL is the de facto standard (many dialects)
|
|
|
|
DOCUMENT DATA MODEL
- Embed data hierarchy into a single object❌
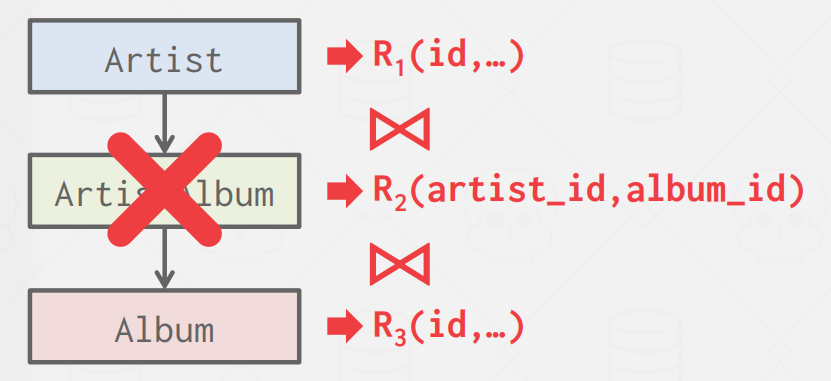
|
|
$$ \Downarrow $$
|
|
CONCLUSION
-
Databases are ubiquitous
-
Relational algebra defines the primitives for processing queries on a relational database.
-
We will see relational algebra again when we talk about query optimization + execution