CMU 15-445 Database Systems

Lecture #11: Joins Algorithms

Introduction

• 根据数据库的范式理论，设计数据库表的一个原则是不让数据冗余，所以在查找的时候JOIN的操作是少不了的

• For binary joins, we often prefer the left table (the ”outer table” ) to be the smaller one of the two.优化SQL的一个方法，左表尽量小(这个小指的是文件页数少)，后面会说明原因

Join Operators

• Operator Output
  • 两个表满足JOIN条件的attributes可以组合成一个新的tuple
  • 输出取决于以下几个方面
    • processing model
    • storage model
    • data requirements in query
  • Data
    • Early materialization

      • 

      • 可以避免子操作回表
    • Record Id

      • 

• Cost Analysis

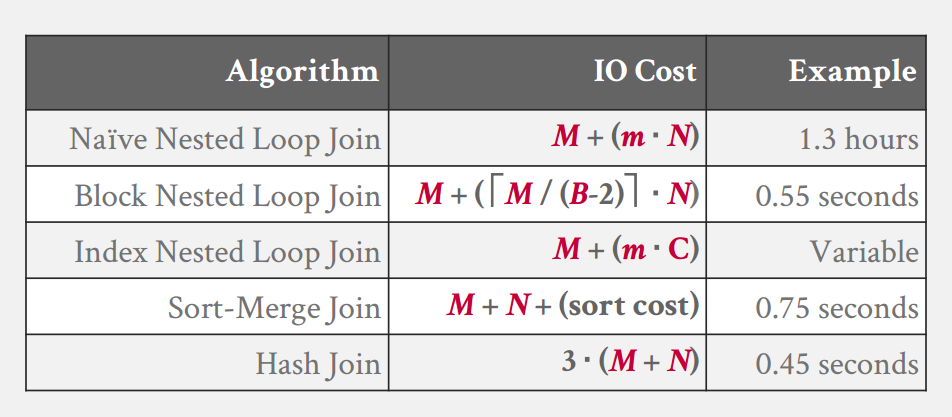
  • 不同JOIN算法的开销

  • Assume

    • M pages in table R, m tuples in R

    • N pages in table S, n tuples in S

    • 1 2 3 4

      SELECT R.id, S.cdate FROM R JOIN S ON R.id = S.id WHERE S.value > 100;

  • Cost Metric: number of IOs to compute join

  • JOIN Algorithms

    • Next Loop Join
    • Sort-Merge Join
    • Hash Join

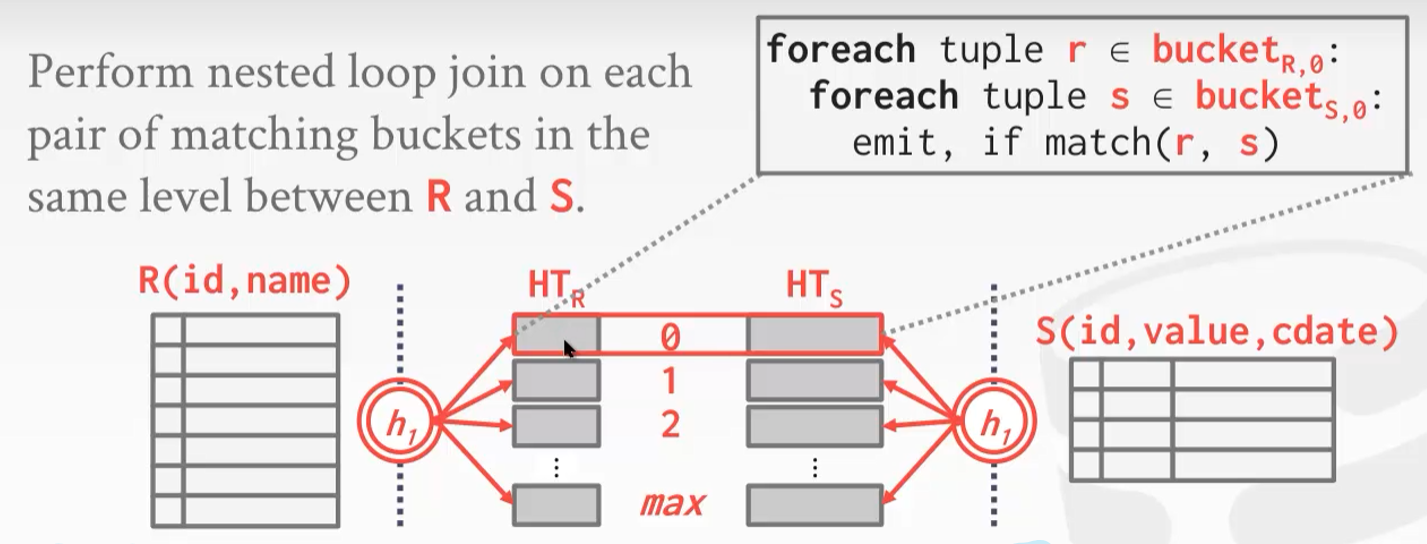
Nested Loop Join

• Native Nested Loop Join
• 伪代码

1
2
3
4
5
6
7

foreach tuple r in R {
    foreach tuple s in S {
        if r and s match {
            emit;
        }
    }
}

• “stupid nested loop join”

  • 一个R中的tuple需要扫S表的所有数据，对于缓存池的利用率过低，这种方法开销太大
  • S每次都是先灌满缓存池，然后前面的页淘汰，如此反复

• Assume

  • M pages in table R, m tuples in R

  • N pages in table S, n tuples in S

• Cost: $M+(m \times N)$

• 优化：高效利用缓存池，一次多加载一些页，不要一页一页加载

• Block Nested Loop Join

• 伪代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

foreach block B_R in R {
    foreach block B_S in S {
        foreach tuple r in B_R {
            foreach tuple s in B_S {
                if r and s match {
                    emit;
                }
            }
        }
    }
}

• 每次不只读一页，每次R和S都读好多页进行匹配

• Cost: $M+(\frac{M}{M\ Block\ Size} \times N)$

• 讨论block size

• B个页的内存，一个页做输出缓存，一个页给右表，多缓存左表(给B-2个)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

foreach B-2 blocks B_R in R {
    foreach block B_S in S {
        foreach tuple r in B-2 blocks {
            foreach tuple s in B_S {
                if r and s match {
                    emit;
                }
            }
        }
    }
}

• Cost: $M+(\frac{M}{B-2}\times N)$

• if $B-2>M$, then cost: $M+N$

• 为啥nested loop join性能不行

  • 总要去遍历S表
  • 为啥要遍历：没有索引等其他方案来提高查找S中属性的效率，所以只能傻瓜式的遍历

• 优化思路：提高S中查找/范围查找的速度

• Index Nested Loop Join

1
2
3
4
5
6
7

foreach tuple r in R {
    foreach tuple S in Index(r[i] == s[j]) {
        if r and s match {
            emit;
        }
    }
}

• 认为每次索引查询需要C次I/O

• Cost: $M+(m\times C)$

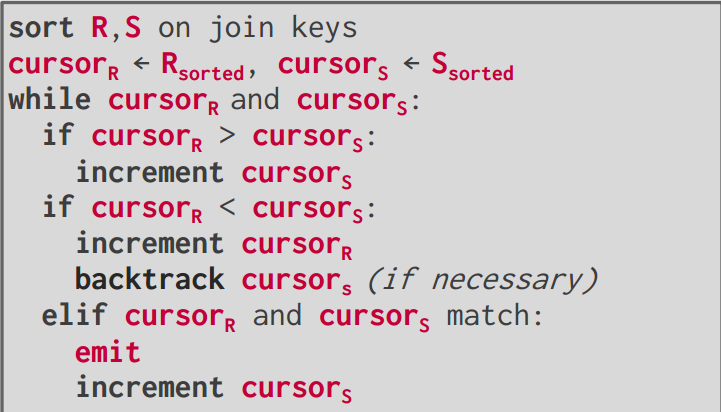
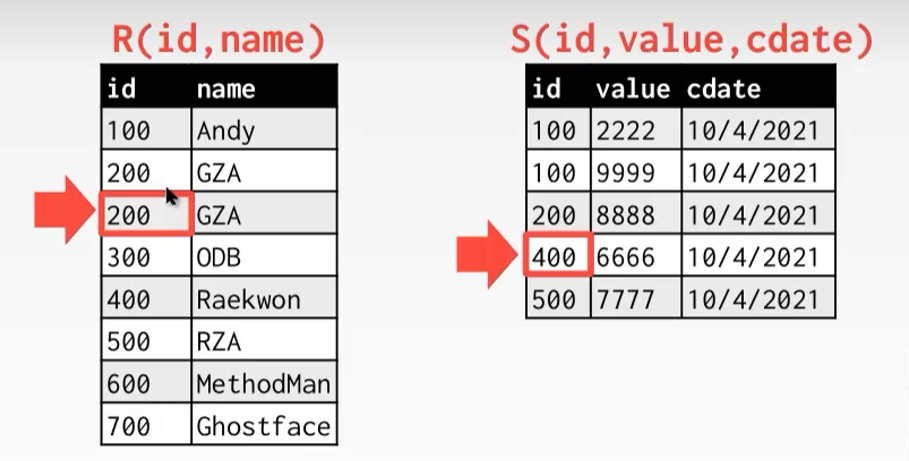
Sort-Merge Join

• Cost

  • Sort R: $2M \times (1+\log_{B-1}\frac{M}{B})$

  • Sort S: $2N\times (1+\log_{B-1}\frac{N}{B})$

  • Merge Cost: $M+N$

  • Total Cost: $Sort + Merge$

• 退化情况：两个连接列所有值一样，那么Merge Cost会因为回退增加到$M\times N$

• 适合的场景

  • 数据本身就有序
  • 输出的结果需要排序

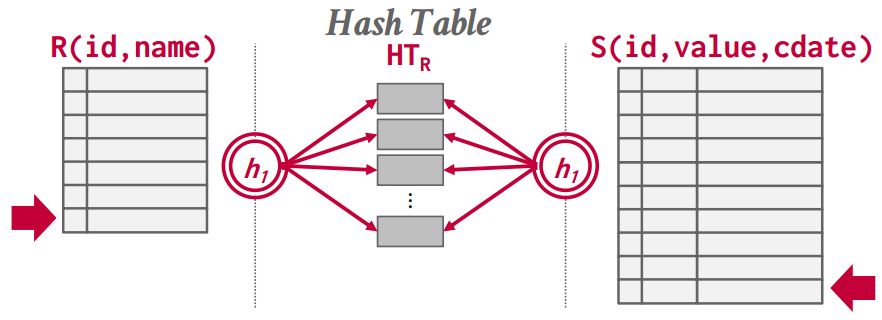
Hash Join

• Hash table点查询比B+ Tree快
  • 左表做hash，右表去匹配

1
2
3
4

build hash table HT_R for R
foreach tuple s in S:
    if h1(s) in HT_R:
        output

• Hash

  • Key:需要连接的列
  • Value
    • Full Tuple:放上需要的数据，不需要回表
    • Tuple Identifier:放索引，最后需要去回表拿数据

• OPTIMIZATION

  • Create a probe filter (such as a Bloom Filter) during the build phase if the key is likely to not exist in the inner relation 加上一层过滤器先过滤掉部分没有匹配项的数据，防止在哈希表里面找半天发现没有，比如加一个布隆过滤器

• 如果哈希表太大可能会面临内存池驱逐的问题，但是我们不想让内存池随机驱逐

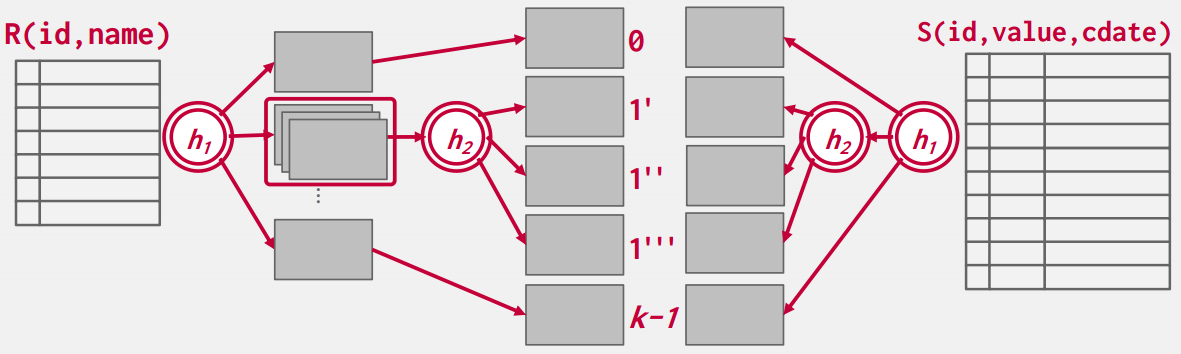
• Grace Hash Join

  • 1980’s东京大学搞数据库一体机的时候发明的（现在也有一体机，比如Oracle还在卖），银行和金融机构爱买

  • 左表和右表都做hash，把哈希表存在硬盘里面，把硬盘里面相对应的哈希桶拿出来做nested loop join

  • 

  • 如果哈希桶还是太大怎么办，再换别的哈希函数继续哈希，直到哈希出来的块够小（这个叫RECURSIVE PARTITIONING）

  • 

• Cost

  • Partition Phash:$2(M+N)$(读到内存hash后还要写回去)
  • Probing Phash:$M+N$
  • Total:$3(M+N)$

Conclusion

• Sorting和Hash没有最好，要看条件选择
  • 哈希碰撞，输出是否有序都会影响开销
  • 优秀的数据库会有优化器来进行分析和选择